Kétezer-kétszáz éves Pascal-háromszög?

Lapszám: Válság – 13 – XIII/1 – 2010 április
Szerző: Śacīsuta dāsa (Tóth Zoltán)
Cikk letöltése pdf-ben: Kétezer-kétszáz éves Pascal-háromszög?

Két fontos esemény inspirált arra, hogy megírjam ezt a rövid tanulmányt. Egyrészt készülök kiadni egy összefoglaló művet erről a témáról, amelyben az alapismereteket követően bemutatom az eddig összegyűjtött, közel 1000 versmértéket. Másrészt pedig, több érdekesség felvonultatása között, külön fejezetben szólok majd egy megdöbbentő felfedezésről, amelyet ugyan a legutóbbi cikkemben is megemlítettem egy rövid bekezdés erejéig, de a legújabb kutatások eredményeinek gazdagsága és elsöprő ereje egy különálló fejezetté növelte ezt a néhány sort a leendő könyvemben. Ezt adom most közre ebben az írásban.

Egy korábbi Tattva-cikkben¹már írtam egy rövid bevezetést a szanszkrit klasszikus verstanba, s ott elmagyaráztam e tudomány alapfogalmait. Mivel nem akarom a kedves olvasót azzal terhelni, hogy egy másik könyvet is lapozgatnia kelljen a szanszkrit szavak értelmezése miatt, ezért ismét leírom ezeket az ismereteket egy külön alpontban.

1. A felfedezés

A 2007-es Tattva-cikkemben az alábbiakat írtam Piṅgaláról:

„Piṅgalát tekintik a bináris számrendszer első alkalmazójának, melyet a védikus versmértékek rendszerén keresztül ismertetett. A versmértékekről szóló munkájában ír a mātrā-meruról (a Fibonacci-számsorról) és a meru-prastāráról (a Pascal-háromszögről) is.”²

Subhash Kak indiai nemzetiségű professzor egyik rövid írására hivatkoztam, akivel az idén nyáron volt szerencsém személyesen is találkozni egy nemzetközi csillagászati konferencia alkalmával, amelyet az MTA szervezett. Akkor megemlítettem neki, hogy nem találom Piṅgala (i.e. 5. sz. vagy i.e. 2. sz.) művében a Pascal-háromszöget, s megadta egy másik indiai tudós, Shyam Lal Singh elérhetőségét, aki erről írt könyvet. Útmutatásával sikerült felvennem a kapcsolatot Shyam Lal Singh professzorral, aki elküldte a Pascal-háromszögről szóló könyvét.

A címben azt írtam, hogy 2200 éves Pascal-háromszöget fogok bemutatni, mert ha találunk is valami rövid leírást Piṅgaláról, a legóvatosabb becslések is az i. e. 2. századra helyezik munkásságát. Kapil Deva Dvivedi (1918-) és Shyam Lal Singh (1942-) professzorok viszont a The Prosody of Piṅgala című munkájuk előszavában azt írják, hogy Piṅgala i. e. 750 körül született, majd azt is megemlítik, hogy a Yudhiṣṭhira Mimānsaka a Vaidika-chandomimānsakában ezt az időpontot kategorikusan i. e. 2850-re teszi.³ Ebből is látható, hogy milyen nehezen datálhatók a prehisztorikus indiai tudósok; a jelen cikknek viszont nem célja a különféle forrásművek és íróik datálása.

A Piṅgala-chandaḥ-śāstra nyolcadik fejezetében Piṅgala ír a Pascal-háromszögről és a Fibonacci-számsorról. Ez az utolsó és egyben a legkevésbé érthető fejezet – s ez nem meglepő, ugyanis Piṅgala egész műve hemzseg a kriptogrammákat is megszégyenítő nyelvtörő sūtráktól. Ezért is lehet, hogy a híres indiai matematikus, Halāyudha Bhaṭṭa (10. sz.) magyarázatai nélkül – melyek i.sz. 975 körül születtek⁴ – az ember sokszor elveszettnek érzi magát. A mű 31. és 35. sūtrájában és azok magyarázataiban a Pascal-háromszög egyik legősibb leírásáról olvashatunk, amelyet legalább 1800 évvel Blaise Pascal⁵ (1623-1662) előtt vetettek papírra.

2. A magyarázat

Piṅgala sūtrái közvetve írják le a Pascal-háromszöget, ezért Halāyudha Bhaṭṭa magyarázatain keresztül fogom bemutatni azt. Előtte viszont megnézzük, hogy miként lehet értelmezni Piṅgala néhány sūtráját, s hogy milyen további sejtéseket vet fel ez a módszer a könyv végén található sūtrákkal kapcsolatban.

Annak érdekében viszont, hogy ne kelljen előkeresni a 2007-es Tattva-cikkemet, a 2.1. alpontban – szinte változatlan formában – újra bemutatom a versmértékekkel kapcsolatos alapismereteket.

2.1. Az akṣara, a mātrā és a gaṇa fogalma

A szanszkrit nyelv lejegyzésére leggyakrabban a devanāgarī írásmódot használják. Az írás legkisebb egysége általában a betű, amelyet a-kṣarának („amit nem lehet tovább osztani”)⁶ neveznek. A devanāgarī írásban a legkisebb egységet a ligatúra⁷ jelenti, amelyet így szintén akṣarának neveznek. Mivel a ligatúrák nem hangokat, hanem szótagokat jelölnek, az akṣara szót itt most „szótag” értelemben használom.

A szanszkrit nyelvben, s gyakorlatilag minden más nyelvben is, a szótagok kiejtése egységnyi időt vesz igénybe. Ez az időegység a mora, amit szanszkritul mātrānak neveznek. Az egy mātrā hosszú szótagot laghunak (kicsi, rövid), a két mātrā hosszút pedig gurunak (nagy, hosszú) nevezik. Három mātrā hosszúságú szótagokat csak énekekben használnak, vagy ha valakit a távolból hívnak (pl.: he rādhe-e-e).⁸ Érdekes és szemléletes példa e három időegység bemutatására a kakaskukorékolás: ku-kuri-kúú. Itt az első szótag egy, a második és a harmadik szótag kettő, míg a negyedik szótag három mātrā hosszú.

A laghu szótagot ez alapján rövidnek, a guru szótagot pedig hosszúnak hívják.

A következő jelöléseket alkalmazom a továbbiakban:
● laghu
− guru

Általában akkor rövid egy szótag, ha rövid magánhangzót, és akkor hosszú, ha hosszú magánhangzót tartalmaz.

A rövid magánhangzók: a, i, u, ṛ, ḷ.

A hosszú magánhangzók: ā, ī, ū, ṝ, ḹ, e, ai, o, au.⁹

A rövid magánhangzót tartalmazó szótagok is hosszúvá válnak az alábbi két esetben:
a) A rövid magánhangzót ṁ (anusvāra) vagy ḥ (visarga) követi. Például:
_{− −}
haṁ – saḥ.
b) A rövid magánhangzót két vagy több mássalhangzó követi. Például:
_{− ●}
kṛ- ṣṇa.

A b) szabály alól kivételt képezhetnek a -pr-, -hr-, -br- és -kr- mássalhangzótorlódások, s ez egyfajta engedményt jelent a költők számára. Ekkor a szótag esetenként rövidnek tekinthető annak érdekében, hogy a versszak megfeleljen a verselés szabályainak. Ezenkívül a negyedvers utolsó szótagja szintén hosszúnak számít, de ha a versmérték úgy kívánja, akkor rövidnek tekintik, függetlenül attól, hogy rövid vagy hosszú magánhangzó szerepel-e a negyedvers végén.¹⁰

Az alábbi példával áttekintjük a legfontosabb szabályokat:
_{● − − ● ● − − − − ● − ● ● – ● −}
hare kṛṣṇa hare kṛṣṇa kṛṣṇa kṛṣṇa hare hare |
_{● – – ● ● – – – – ● – ● ● – ● –}
hare rāma hare rāma rāma rāma hare hare ||

A versmértékek elemzésének megkönnyítése érdekében a szakértők nyolc gaṇát, azaz verslábat határoztak meg, melyek mindegyike három-három szótagot tartalmaz. A különféle gaṇákat különböző betűkkel jelölik, melynek alapján a következő táblázatot állíthatjuk össze:

szanszkrit elnevezés	gaṇa	görög-latin elnevezés¹¹
ya-gaṇa	● − −	bacchius
ra-gaṇa	− ● −	krétikus
ta-gaṇa	− − ●	palimbacchius
bha-gaṇa	− ● ●	daktilus
ja-gaṇa	● − ●	amphibrachisz
sa-gaṇa	● ● −	anapesztus
ma-gaṇa	− − −	molosszus
na-gaṇa	● ● ●	tribrachisz

Ezenkívül a rövid szótagot la (laghu), a hosszút pedig ga (guru) betűkkel jelölik. A verstani szövegek ezeket szintén gaṇaként szokták megemlíteni: la-gaṇa, ga-gaṇa. Akkor kapnak leginkább szerepet a leírásokban ezek az egyszótagú gaṇák, amikor a versmértékek szótagjainak a száma nem osztható hárommal.

A verselésről szóló nyugati szakirodalom közel negyven vers-lábat tart számon. A szanszkrit versmértékeket leíró gaṇák rend-szere egyszerűbb, mint a nyugati verslábak gyűjteménye, mert pusztán e nyolc gaṇa segítségével – kiegészítve a la- és a ga-gaṇával – bármilyen versmérték leírható. Például a choriambus elnevezésű versláb (− ● ● −) a következőképpen kódolható egyszerűen a gaṇák segítségével: bha, ga.

2.2. Piṅgala rejtjeles sūtrái

Az alapismeretek áttekintését követően térjünk vissza a Piṅgala-sūtrákhoz!
A Piṅgala-chandaḥ-śāstra legelső sūtrája így néz ki: dhī-śrī-strī m¹². Az első három szó jelentése a következő:
dhī = értelem, bölcsesség
śrī = szépség, ragyogás, dicsőség
strī = nő, feleség
Mielőtt még belebonyolódnánk a fenti jelentéstartalmak összehangolásába, gondolkozzunk el egy pillanatra a sūtra végén szereplő m betűn. Mit jelenthet?

A versmértékek szakértői tudják, hogy minden chandaḥ-śāstra elején definiálják a gaṇákat. Ebben a sūtrában az m betű így a ma-gaṇára utal, az előtte lévő szavakat pedig teljes mértékben felesleges lefordítani. Nézzük csak meg a sūtra versképletét!

_{− − −}
dhī-śrī-strī m ||

Tehát megtaláltuk az első gaṇa képletét, a ma-gaṇa ugyanis pontosan három hosszú szótagból áll. Az m betű előtt szereplő szavaknak tehát elsősorban az a funkciójuk, hogy kódolják a gaṇa képletét. S mivel mind közismert szavak, ezért ha valamelyik másoló az évszázadok során hibát vét a sūtrák átírása során, könnyű kijavítani később a hibát.

Az első tíz sūtrát¹³ennek megfelelően már könnyű értelmezni:
(1) dhī-śrī-strī m || ma-gaṇa − − −
(2) varā sā y || ya-gaṇa ● − −
(3) kā guhā r || ra-gaṇa − ● −
(4) vasudhā s || sa-gaṇa ● ● −
(5) sā te kva t || ta-gaṇa − − ●
(6) kadā sa j || ja-gaṇa ● − ●
(7) kiṁ vada bh || bha-gaṇa − ● ●
(8) na hasa n || na-gaṇa ● ● ●
(9) gṛ l || la-gaṇa ●
(10) g ante || ga-gaṇa −

A tizedik sūtra már nem csupán kódol, hanem jelzi is, hogy itt a vége (ante) a gaṇák felsorolásának. Hiába áll ugyanis két hosszú szótagból, a ga-gaṇa köztudottan egyetlen egy hosszú szótagot jelöl.

Ez csupán egy rövid betekintő volt a Piṅgala-sūtrák világába. A nyolcadik fejezet végén egyelőre csak utalásokat találtam a kettes számrendszerre a śūnyam=üres (nulla) és a pūrṇa=teli (egy) szavak ismétlődése révén. A Pascal-háromszögre, vagy ahogy ők nevezik, a meru-prastārára szintén csak utalásokat találtam, konkrétan csak Halāyudha Bhaṭṭa írja le sorról-sorra. Az viszont biztos, hogy ezt a meru-prastārát¹⁴ arra használták, hogy előállíthassák és megszámolják a samacatuṣpadī¹⁵ versmértékek összes lehetséges variánsát. Ezt mutatom be a következő alpontban.

2.3. A meru-prastāra mint Pascal háromszög

Halāyudha Bhaṭṭa rendkívüli logikával építi fel a Pascal háromszöget, vagy ahogy ő nevezi: a meru-prastārát.¹⁶ Először a sorok összesítését – amelyek kettő hatványainak felelnek meg – adja meg Piṅgala 8.31-es sūtrájához fűzött magyarázatában.¹⁷ Ezek a számok megmutatják, hogy az egyes samavṛtti versmértékcsoportok összesen hányféle versmértéket tartalmazhatnak, ha figyelembe vesszük a rövid és a hosszú szótagok összes lehetséges variációját.

Így ír: tato dvau dvābhyāṁ guṇitau catvāro bhavanti¹⁸. Vagyis a kétszótagú versek négyfélék lehetnek: 1) mindkét szótag hosszú; 2) az első szótag rövid és a második hosszú; 3) az első szótag hosszú és a második rövid; 4) mindkét szótag rövid. Ez az összes variációs lehetőség a kétszótagú versek esetében.

Később, ugyanebben a magyarázatban már megemlíti a versmértékcsoport neveit is a gāyatrīval (6) kezdve: tato ‘ṣṭāv aṣṭābhir guṇitāṣ catuḥ-ṣaṣṭir bhavanti gāyatrī samavṛttāni. Azaz a samavṛtti osztály gāyatrī elnevezésű, hatszótagú versmértékcsoportjába tartozó versmértékek összes lehetséges száma 64 (catuḥ-ṣaṣṭiḥ). Majd így folytatja: anenaiva nyāyenāṣṭāviṁśaty adhika śatam uṣṇinaḥ. Az uṣṇik (7) versmértékcsoport versmértékeinek összes lehetséges száma 128 (aṣṭāviṁśaty adhika śatam).

Aztán egyre szűkszavúbb, már csak a lényeget említi: ṣat-pañcāśad adhike dve śate anuṣṭubhaḥ. Az anuṣṭubh (8) versmértékcsoportba összesen 256 versmérték tartozhat. Dvādaśottarāṇi pañca śatāni bṛhatyāḥ. A bṛhatī (9) versmértékcsoportba összesen 512. És így számol tovább, egészen 4096-ig, a jagatī versmértékcsoporttal bezáróan. Ennek megfelelően felrajzolom a már jól ismert Pascal háromszöget az ukthā versmértékcsoporttól egészen a jagatīig.

A háromszöget egyébként könnyen fel lehet építeni. A csúcsán egy 1-es áll, alatta pedig mindkét irányba rézsútosan két darab 1-es. Ezek együtt egy háromszöget alkotnak. A következő´ sor széleit szintén 1-esek alkotják, középen viszont egy 2-es található. A 2-est úgy kapjuk meg, hogy összeadjuk a felette lévő´ két számot: 1+1=2. A harmadik sorban már két 3-as szerepel, melyeket két 1-es fog közre két oldalról, mivel 1+2=3, illetve 2+1=3. Így összesen tíz számjegyünk van, melyek együtt ugyancsak egy háromszöget alkotnak. Ezért hívják Pascal-háromszögnek. E számháromszög összeállításának szabályát így ábrázolhatjuk egyszerűen:

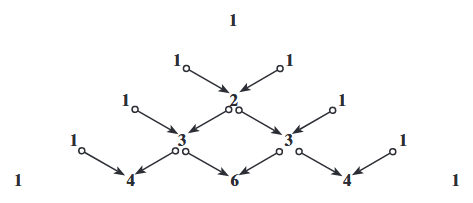
Tehát az első sorban egyedül egy 1-es áll. A második sorban két darab 1-es van, amit össze kell adni: 1+1=2. Ez a második sor eredménye. A harmadik sorban már három számjegy található, melyeket szintén össze kell adni: 1+2+1=4, és így tovább. S ezek az eredmények (1, 2, 4 stb.) rendre a kettő hatványai (2⁰, 2¹, 2² stb.). Hogy mit jelentenek ezek az összeadások, arra a következő alpontban világítok rá.

2.4. A varṇa-meru-prastāra további jellemvonásai

Hiszen ezzel még nem ért véget az érdekességek sora. Ugyanis a háromszög belsejében szereplő számok nemcsak a binominális együtthatók¹⁹ egyszerű kiszámítási módját adják meg, hanem azt is, miként és hányféle módon képezhetők az egyes versmértékek. Nézzük csak meg közelebbről!

Halāyudha Bhaṭṭa a Piṅgala-chandaḥ-śāstra legutolsó, 8.34-es sūtrájának magyarázatában²⁰ rávilágít arra, hogy miként lehet könnyen megalkotni a versmértékeket a szótagszámok ismeretében, s ezzel gyakorlatilag meghatározza a Pascal-háromszöget alkotó összes számot.

E magyarázat vége felé az ukthā (1) versmértékekről így ír: tatraika-gurv eka-laghu vṛttam bhavati. Vagyis összesen kétféle ilyen versmérték létezik: az egyikben egy hosszú (eka-guru), a másikban pedig egy rövid szótag (eka-laghu) található. Ezt mutatja a varṇa-meru-prastāra második sora is: 1, 1.

Az atyukthāk (2) esetében már többféle variáns lehet: tatraikaṁ sarva-guru dve eka-laghunī ekaṁ sarva-laghv iti koṣṭha krameṇa vṛttāni bhavanti. Tehát egy versmérték csupa hosszú szótagból áll (ekaṁ sarva-guru), két versmértékben mindig van egy rövid szótag is (dve eka-laghunī), egy versmérték pedig csupa rövid szótagból áll (ekaṁ sarva-laghu). Erre rímel a varṇa-meru-prastāra harmadik sora: 1, 2, 1.

Most lerajzolom az ukthā és az atyukthā versképleteit:

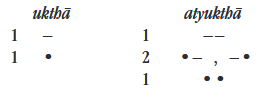
A madhyamāt (3) határozza még meg ilyen részletességgel: tatraikaṁ sarva-guru trīṇy eka-laghūni trīṇi dvi-laghūni ekaṁ sarva-laghu. Vagyis egy versmérték csupa hosszú szótagból áll; három versmérték tartalmaz egy rövid szótagot, miközben a másik kettő csak hosszú lehet; három versmérték két rövid szótagot tartalmaz, és csak egy hosszú szótag található benne; s végül egy csupa rövidszótagos versmérték van ebben a versmértékcsoportban. Ennek megfelelően a varṇa-meru-prastāra negyedik sorában ez áll: 1, 3, 3, 1. Ábrázolva:

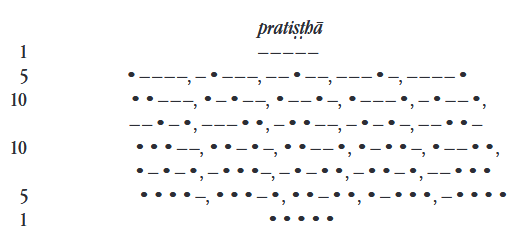
Halāyudha Bhaṭṭa ezután már nem részletezi a további sorokat, hanem csak megemlíti a szabályszerűség fő elemeit, hiszen a varṇa-meru-prastāra most már egyértelműen a segítségünkre lesz abban, hogy egyetlen versmérték se maradjon ki a gyűjteményből. Az eddigi ismeretek birtokában könnyedén összeállíthatjuk magunknak az ötödik sor alapján (1, 5, 10, 10, 5, 1) a pratiṣṭhā (4) versmértékcsoport lehetséges variánsait. Íme:

3. Konklúzió

Szembetűnő tehát, hogy a Pascal-háromszögként ismert varṇa-meru-prastāra milyen sokoldalúan járul hozzá a samacatuṣpadī versmértékek összes lehetséges variánsának kiszámításához. Segítségével hosszú évszázadokon keresztül sikeresen állították elő a legkülönfélébb akṣara vagy vṛtti típusú versmértékeket. Nincs arról tudomásom, hogy használták volna ezt a módszert Indiában több ezer évvel ezelőtt a matematika terén a binominális együtthatók kiszámításához, mindenesetre érdekes tény, hogy milyen ötletes módon oldották meg már akkor a verstannal kapcsolatos kombinatorikai²¹ feladatokat.

Lehet, hogy a Piṅgala-chandaḥ-śāstrában nem találunk részletes leírást a Pascal-háromszögről, de az alábbiakat mindenképp érdemes fontolóra vennünk:

1) A Piṅgala-chandaḥ-śāstra kizárólag sūtrákból áll, mely irodalmi stílus nem támogatja a minden részletre kiterjedő bemutatásokat, hanem éppen ellenkezőleg: minél rövidebb, tömörebb kifejezésmódot igényel. Ezért nem ritka, hogy a sūtrákból álló művek (mint például a Vedānta-sūtra) nehezen értelmezhetők, és emiatt minden esetben hozzáértő magyarázatokra van szükség.

2) Semmi okunk nincs arra, hogy azt feltételezzük: Piṅgala nem ismerte a versmértékcsoportok variánsainak a kiszámítási módját. Halāyudha magyarázatai ennek az ellenkezőjét támasztják alá, s ebből az következik, hogy a varṇa-meru-prastārát már legalább 2200 éve használják Indiában.

Ez volt röviden a Pascal-háromszög indiai története. A Fibonacci-számsorról a most készülő könyvemben lehet majd olvasni, s abból megtudhatjuk, hogy az is legalább ilyen ősi, és ugyancsak a versmértékekkel kapcsolatban használták.

LÁBJEGYZET

¹ TATTVA.
² TATTVA :116.
³ Dvivedi-Singh 2008: xxii-xxiii.
⁴ Dvivedi-Singh 2008: xxiii.
⁵ Blaise Pascal 1655-ben publikált először ebben a témában a Traité du triangle arithmétique című értekezésében.
⁶ Harivenu 2005: 20.
⁷ Ligatúra: a szótag lejegyzésére szolgáló írásjel a szanszkrit nyelvben.
⁸ Harivenu 2005: 20.
⁹ A szanszkritban az ‘e‘ és az ‘o‘ mindig hosszú ‘é’-t és ‘ó’-t jelent. Az ‘ai‘ és az ‘au‘ együtt szintén hosszú magánhangzónak számít.
¹⁰ Apte 2000: 1035.
¹¹ Szepes-Szerdahelyi 1981: 191.
¹² Piṅgala 2002: 2.
¹³ Piṅgala 2002: 2-4.
¹⁴ meru=a Meru-hegy; prastāra=kiterjedés, beborítás; a verslábak összes lehetséges társítását tartalmazó táblázat.
¹⁵ samacatuṣpadī (vagy samavṛtti)=olyan versmértékek csoportja, amelyek négy (catur) verssorból (pāda) állnak, s mind a négy verssor azonos (sama) versképlettel bír.
¹⁶ A Vṛttaratnākara (6.7 magyarázat, 201. o.) és a Chandaḥ-Kaustubha (8.6 és magyarázat, 210-211. o.) varṇa-meru-prastāraként említi, mivel létezik egy másik fajta is: a mātrā-meru-prastāra. A varṇa-meru-prastāra a Pascal-háromszöget adja meg, a mātrā-meru-prastāra pedig a Fibonacci számsort. A Fibonacci-számsorról egy másik cikkben írok majd.
¹⁷ Piṅgala2002: 193-194.
¹⁸ Az aláhúzások itt és a többi idézetben is mind tőlem származnak.
¹⁹ A binominális együtthatókat legegyszerűbben az alábbi matematikai formulákkal tudom bemutatni.
A Pascal-háromszög csúcsa (1) a következő matematikai kifejezés eredménye: (x+y)⁰ = 1.
A Pascal-háromszög második sora (1 1) az ‘x’ és az ‘y’ ismeretlenek tényezői, amelyeket most a szemléltetés kedvéért kiírok: (x+y)¹ = 1x+1y.
A harmadik sor (1 2 1) így néz ki: (x+y)² = 1x²+2xy+1y².
A negyedik sor (1 3 3 1) így néz ki: (x+y)³ = 1x³+3x²y+ 3xy²+1y³.
Az ötödik sor (1 4 6 4 1) pedig így néz ki: (x+y)⁴ = 1x⁴+4x³y+6x²y²+4xy³+1y⁴.
És így tovább.
²⁰ Piṅgala2002: 195.
²¹ A kombinatorika a matematika azon területe, amely egy véges halmaz elemeinek valamilyen szabály alapján történő csoportosításával, kiválasztásával, sorrendbe rakásával foglalkozik. Az elemi kombinatorika tárgyai a permutációk, kombinációk és variációk.

FELHASZNÁLT IRODALOM

Apte, Vaman Shivram 2000: The Student’s Sanskrit-English Dictionary. Delhi, Motilal Banarsidass Publishers.
Harivenu das 2005: Sanskrit Bhagavad-gītā grammar. India, Bhaktivedanta Svāmī Language School.
Kapil Deva Dvivedi, Dr.-Shyam Lal Singh, Dr. 2008: The Prosody of Piṅgala. Vārāṇasī, Vishwavidyalaya Prakashan.
Kedāra Bhaṭṭa 2004: Vṛttaratnākara (with the commentaries of Bhaṭṭa Nārāyaṇa Bhaṭṭ edited with the Maṇimayī commentary in Hindi by Pt. Śrī Kedāra Nātha Śarmā; The Kashi Sanskrit Series 55). India, Caukhambhā Saṁskṛta Saṁsthāna.
Piṅgala 2002: Chandaḥ-śāstram (with the commentary Mṛtasañjīvanī by Śrī Halāyudha Bhaṭṭa; edited by Paṇḍita Kedāranātha). India, Caukhambhā Publishers.
Rādhā Dāmodara Prabhupāda 1990: Chandaḥ Kaustubhaḥ (with the commentary Kṛta-bhāṣyopetaḥ by Śrīmad Baladeva Vidyābhūṣaṇa). Vṛndāvana (India), Haridāsa Śāstrī.
Śacīsuta dāsa (Tóth Zoltán) 2007: Bevezetés a klasszikus szanszkrit verstanba. TATTVA X. 1.
Szepes Erika – Szerdahelyi István 1981: Verstan. Budapest, Gondolat.